Mathe-Abitur: Was du über Themen und Aufgaben wissen musst
Die Prüfung in Mathe gehört zu den wichtigsten Meilensteinen auf dem Weg zu deinem Abitur. Um dich so gut wie möglich darauf vorzubereiten, solltest du dich mit diesen Bereichen auseinandersetzen.
Die Vorbereitung auf deine Abiturprüfung in Mathe 2022 steht an? Dazu haben wir hier die prüfungsrelevanten Themen und Informationen fürs Mathe-Abi für dich zusammengestellt. Außerdem gibt es die Termine fürs Mathe-Abi für alle Bundesländer und einige Bundesländer detaillierte Hinweise.
Übersicht
- Termine fürs Mathe-Abi 2022
- Abitur Mathe 2022: Diese Themen solltest du auf jeden Fall wiederholen
- Aufbau und Schwerpunkte im Mathe-Abitur
- Abi-Hinweise für 2022 nach Bundesländern:
Termine fürs Mathe-Abi 2022
Bundesland Haupttermin Nachschreibetermin Baden-Württemberg 03. Mai 2022 18. Mai 2022 Bayern 03. Mai 2022 k. A. Berlin 03. Mai 2022 25. Mai 2022 Brandenburg 03. Mai 2022 (09:00 Uhr) 25. Mai 2022 (09:00 Uhr) Bremen 03. Mai 2022 23. Mai 2022 Hamburg 20. April bis 05. Mai 2022 30. Mai bis 03. Juni 2022 Hessen 03. Mai 2022 31. Mai 2022 Mecklenburg-Vorpommern 03. Mai 2022 23. Mai 2022 Niedersachsen 03. Mai 2022 23. Mai 2022 Nordrhein-Westfalen 03. Mai 2022 18. Mai 2022 Rheinland-Pfalz 03. Mai 2022 (G8) nicht zentral Saarland 03. Mai 2022 24. Mai bis 02. Juni 2022 Sachsen 03. Mai 2022 24. Mai 2022 Sachsen-Anhalt 25. April bis 06. Mai 2022 k. A. Schleswig-Holstein 03. Mai 2022 k. A. Thüringen 23. Mai 2022 29. Juni 2022 Abitur Mathe 2022: Diese Themen solltest du auf jeden Fall wiederholen
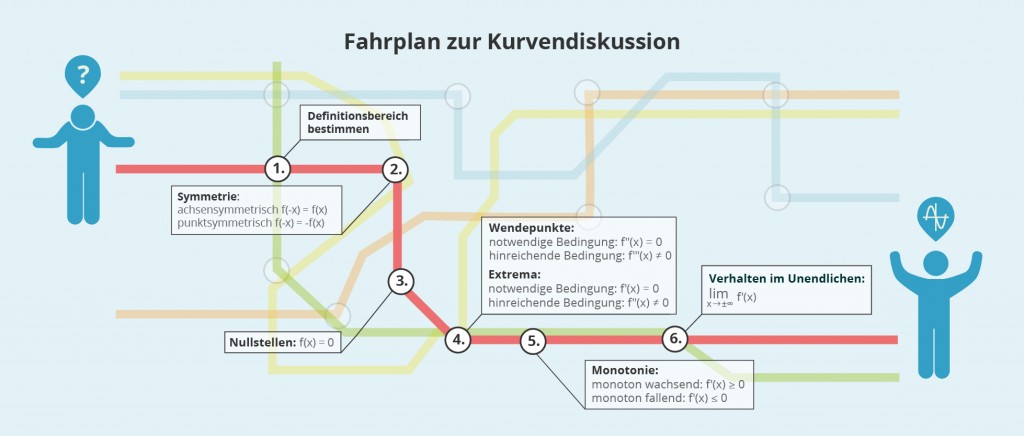
Die Grundbegriffe der Differentialrechnung, wie Differenzenquotient und Differentialquotient, solltest du im Bereich der Analysis kennen, damit du gut auf das Abitur vorbereitet bist. Sicher beherrschen solltest du außerdem die wichtigsten Ableitungsregeln wie die Potenz-, Summen-, Faktor-, Ketten- sowie die Quotientenregel. Fragen nach der Differenzierbarkeit, Stetigkeit, Symmetrie und Monotonie von Funktion solltest du ebenfalls beantworten können. Setze dich zudem mit dem Begriff der Konvergenz und des Grenzwertes von Funktionen und Folgen auseinander. Du solltest wissen, wie du im Abitur bei der Analyse von Funktionen vorgehst. Als Hilfe für die Vorbereitung haben wir dir einen „Fahrplan zur Kurvendiskussion“ erstellt:
Extra-Tipp
Um dich aufs Mathe-Abitur gezielt vorzubereiten, kannst du auch die Abschlussprüfungen auf sofatutor ausprobieren. Hier findest du Übungen und Videos zu allen wichtigen Themenbereichen. Wir wünschen dir viel Erfolg bei deiner Prüfung!
Übersicht zur Kurvendiskussion | ©sofatutor Die verschiedenen Aspekte der Integralrechnung, wie die Rekonstruktion von Beständen sowie die Berechnung von Flächen und auch Volumina von Rotationskörpern, gehören ebenfalls dazu.
Bei der Analytischen Geometrie / Linearen Algebra solltest du Punkte, Geraden und Ebenen mathematisch beschreiben und berechnen können. Dazu gehört, dass du weißt, was man unter einem Vektor versteht und wie man mit diesem operiert. Außerdem solltest du eine Gerade, eine Strecke oder eine Ebene vektoriell darstellen können. Setze dich mit Lagebeziehungen zwischen Punkten, Geraden und Ebenen auseinander und damit, wie man Abstände, Schnittpunkte und Schnittwinkel berechnet.
Erinnerst du dich noch an die Formeln zur Berechnung von Erwartungswert und Varianz? Auch sie können eine Rolle in deiner Prüfung spielen. In der Stochastik solltest du zunächst die Grundlagen wiederholen, z. B. wie die Wahrscheinlichkeit ein- und mehrstufiger Zufallsversuche berechnet wird und wie Baumdiagramme und Vierfeldertafeln eingesetzt werden können. Neben bedingter Wahrscheinlichkeit und der Bernoulli-Formel können dir zusätzlich Wahrscheinlichkeitsverteilungen oder Hypothesentests in der Abiturprüfung begegnen.
Abitur in Mathematik 2022: Aufbau und Schwerpunkte
Die Abiturprüfungen beinhalten verschiedene Aufgaben, die sich auf die drei großen Themenbereiche aus den letzten beiden Jahren der Oberstufe beziehen. Im Grundkurs dauert die Prüfung zwischen 250 bis 270 Minuten und im Leistungskurs 300 bis 330 Minuten. Meistens werden noch 30 Minuten Zeit für die Auswahl der Aufgaben aus dem Wahlteil gewährt.
Allgemeiner Aufbau der schriftlichen Prüfung in Mathematik
Die schriftliche Abiturprüfung besteht aus einer Pflichtaufgabe (A 0 für den Grundkurs oder B 0 für den Leistungskurs) sowie drei Wahlaufgaben für den Prüfungsteil A und zwei Wahlaufgaben für den Prüfungsteil B (nur Leistungskurs). Im Grundkurs bearbeitest du nach der Pflichtaufgabe noch zwei von drei Aufgaben des Prüfungsteils A. Im Leistungskurs beantwortest du darüber hinaus noch eine von zwei Aufgaben aus Aufgabenteil B. Im Grundkurs kannst du insgesamt 90 Punkte in der Prüfung erlangen. Im Leistungskurs kannst du maximal 120 Punkte erlangen.
Zugelassene Hilfsmittel
Als Hilfsmittel zugelassen sind:
- ein Wörterbuch der deutschen Rechtschreibung aus Papier
- ein zweisprachiges Wörterbuch für die Schülerinnen und Schüler, deren Muttersprache nicht Deutsch ist
- der in deiner Jahrgangsstufe eingeführte Taschenrechner (WTR oder mit / ohne CAS)
- einer Merkhilfe (in Bayern und Baden-Württemberg) oder Formelsammlung
- Standard-Zeichenwerkzeuge (z. B. in Brandenburg)
Wichtig: Für die Pflichtaufgabe sind keine Hilfsmittel vorgesehen.
In jedem Bundesland werden Aufgaben aus diesen drei Themenbereichen gewählt:
- Funktionen und Analysis
- Analytische Geometrie und Lineare Algebra
- Stochastik
Extra-Tipp
Um dich aufs Mathe-Abitur gezielt vorzubereiten, kannst du auch die Abschlussprüfungen auf sofatutor ausprobieren. Hier findest du Übungen und Videos zu allen wichtigen Themenbereichen. Wir wünschen dir viel Erfolg bei deiner Prüfung!
Analysis
Die Analysis beschreibt die Untersuchung von Funktionen hinsichtlich ihrer Stetigkeit, Differenzierbarkeit und Integrierbarkeit. Ein wichtiger Schwerpunkt ist dabei die Differentialrechnung mit der Kurvendiskussion. Hier ist ein Beispiel zur Kurvendiskussion:
Download
Lernposter-Beispiel-einer-Kurvendiskussion1.jpg (Dateigröße: 1MB)
Um den Download zu starten, geben Sie Ihre E-Mail-Adresse ein. Klicken Sie anschließend auf „Jetzt herunterladen“.
Danke! Der Download wurde automatisch gestartet.
Differentialrechnung
- Änderungsverhalten von Funktionen
- Grenzwerte von Funktionen: Verhalten im Unendlichen, Grenzwert an einer Stelle, Grenzwertsätze für Funktionen
- Stetigkeit einer Funktion an einer Stelle, in einem Intervall und im Definitionsbereich
- lokales Differenzieren:
- Differenzenquotient und seine Deutung als Sekantenanstieg / mittlere Änderungsrate
- Differentialquotient und seine Deutung als Tangentenanstieg / lokale Änderungsrate
- globales Differenzieren:
- Ableitungsfunktion
- Ableitung ganzrationaler Funktionen: Summenregel, Produktregel
- Ableitung von gebrochen-rationalen Funktionen: Quotientenregel
- Ableitung von Exponentialfunktionen
- Ableitung von verketteten Funktionen: Kettenregel
- weitere Ableitungsregeln: Ableitung der Sinus- und Kosinusfunktion, Wurzelfunktion und von Potenzfunktionen mit rationalen Exponenten
- Graphen gebrochen-rationaler Funktionen: Grenzwertbegriff, Polstellen, horizontale und vertikale Asymptoten
- natürliche Exponential- und Logarithmusfunktion und ihre Ableitungen
Integralrechnung
- Stammfunktion und unbestimmtes Integral:
- Begriff der Stammfunktion
- Ermitteln von Stammfunktionstermen
- Flächeninhalt und bestimmtes Integral:
- bestimmtes Integral und Integralfunktion
- Hauptsatz der Differential- und Integralrechnung
- Berechnung von Flächeninhalten …
- zwischen x-Achse und Funktion
- zwischen zwei Funktionen
- Ermitteln von Integralen mit und ohne Hilfsmittel:
- Integration von ganzrationalen Funktionen
- Integration von Potenzfunktionen mit rationalen Exponenten
- Integration verknüpfter Funktionen
- Integration mittels Substitution und partieller Integration
- Eigenschaften des bestimmten Integrals
- Rotationsvolumen bei Rotation einer Funktion um die Abszissenachse
- Zusammenhänge zwischen Graphen von Funktionen, Ableitungsfunktion und Integralfunktion: graphisches Differenzieren und Integrieren
Anwendungen der Differential- und Integralrechnung
- Wachstums- und Zerfallprozesse
- Untersuchungen an verknüpften Funktionen
- Extremwertprobleme
- Kurvenrekonstruktionen
- Kurvendiskussion
Analytische Geometrie / Lineare Algebra
Die analytische Geometrie löst geometrische Probleme mithilfe von Algebra. Das meint, dass geometrische Aufgaben rechnerisch und nicht zwangsläufig zeichnerisch zu lösen sind.
Lineare Gleichungssysteme
- mit zwei Variablen
- Gleichsetzungsverfahren
- Additionsverfahren
- Einsetzungsverfahren
- Gauß-Verfahren
- zeichnerische Lösung
Koordinatengeometrie im Raum
- Darstellen von Punkten, Vektoren und einfachen Körpern
- Rechnen mit Vektoren:
- Addition, Subtraktion und Vielfachenbildung von Vektoren
- Anwendungen von Skalar- und Vektorprodukt
- lineare Abhängigkeit und Unabhängigkeit von Vektoren
- Orthogonalitätsbedingung für Vektoren, Normalenvektor
Geraden und Ebenen im Raum
- Gleichungen von Geraden und Ebenen in Parameterform und in parameterfreier Form
- Lagebeziehungen:
- gegenseitige Lage von Geraden
- gegenseitige Lage von Ebenen sowie von Geraden und Ebenen zueinander
- Abstände und Winkel:
- Hessesche Normalenform für Ebenengleichungen
- Schnittwinkel: Gerade – Gerade, Gerade – Ebene, Ebene – Ebene
- Abstände: Punkt – Punkt, Punkt – Gerade, Punkt – Ebene, Gerade – Ebene, Gerade – Gerade, Ebene – Ebene
- Schnitt- und Spurpunkte
Stochastik
Die Stochastik (lat. „Ratekunst“) beschreibt die mathematischen Bereiche der Wahrscheinlichkeitstheorie und der mathematischen Statistik.
Binomialverteilte Zufallsgrößen
- Wahrscheinlichkeiten mehrstufiger Zufallsexperimente:
- Pfadregeln
- Abzählverfahren
- Urnenmodell für das Ziehen mit und ohne Zurücklegen
- Baumdiagramme
- Erwartungswert, Varianz und Standardabweichung
- Bernoulli-Experiment und -Kette
- Binomialkoeffizient und Binomialverteilung
- bedingte Wahrscheinlichkeit: Satz von Bayes
- stochastische Unabhängigkeit von Ereignissen und Zufallsgröße
- ein- und zweiseitiger Signifikanztest
Normalverteilte Zufallsgrößen
- Schließen von einer Zufallsstichprobe auf die Grundgesamtheit
- Wahlprognosen durch Hochrechnung, Angabe von Messergebnissen
- Stichprobenmittel und Stichprobenvarianz
- statistische Sicherheit
- ein- und zweiseitiger Signifikanztest:
- Nullhypothese, Testgröße
- Signifikanzniveau, kritischer Wert
- Ablehnungsbereich, Entscheidungsregel
- Fehler 1. und 2. Art
- Sigma-Regeln für prognostische Aussagen
Hinweise zum Mathematik-Abitur für einzelne Bundesländer
Damit du dich noch besser auf die Aufgaben und Themen in der Mathematik-Abiturprüfung in deinem Bundesland vorbereiten kannst, solltest du dir die einzelnen Vorgaben genau lesen. Meistens musst du weniger können, als in den Teilbereichen aufgeführt wurde.
Nachfolgend findest du genauere Angaben zu den Themen im Abitur in Mathe 2022 für Baden-Württemberg, Berlin und Brandenburg.
Abitur Mathematik 2022 Baden-Württemberg
Einige Themen, die du im Unterricht wahrscheinlich gelernt hast, sind im Abitur in Baden-Württemberg nicht prüfungsrelevant. In deiner schriftlichen Prüfung werden Folgen und Iterationen nicht vorkommen. Ebenso kannst du Differenzialgleichungen, das Verfahren des geschlossenen Vektorzugs sowie mehrfaches Quadrieren (bei mehreren Wurzeltermen)
und die Optimierung bei Wurzelfunktionen mit Mitteln der Differentialrechnung bei deiner Vorbereitung außer Acht lassen. In Baden-Württemberg ist diese Merkhilfe für deine Abiturprüfung in Mathematik zulässig. Themen, die du beherrschen solltest sind: Potenzfunktionen, ganzrationale und trigonometrische Funktionen, natürliche Exponentialfunktionen sowie einfach gebrochen-rationale Funktionen.Bei der Wirkung von Parametern sind insbesondere die Verschiebung sowie Streckungen und Spiegelungen in der X- und Y-Richtung wichtig. Du solltest ebenso alle Ableitungsregeln, also Summen- und Faktorregel, Ketten-, Produkt- und Potenzregel, beherrschen.
Integrale und Integralfunktionen sind ebenso relevant wie die Untersuchung von Funktionen und Graphen, z. B. Bestimmung von Nullstellen, Grenzverhalten sowie Extrem- und Wendepunkten. Weitere Themen findest du in der Übersicht zum schriftlichen Abitur für 2022.
Extra-Tipp
Um dich aufs Mathe-Abitur gezielt vorzubereiten, kannst du auch die Abschlussprüfungen auf sofatutor ausprobieren. Hier findest du Übungen und Videos zu allen wichtigen Themenbereichen. Wir wünschen dir viel Erfolg bei deiner Prüfung!
Abitur Mathematik 2022 Berlin & Brandenburg
Du musst für die Abiturprüfung nicht alle Themen beherrschen, die du im Unterricht behandelt hast. So ist die Erläuterung und Entwicklung von Beweisen und das Nutzen von Grenzwerten bei der Bestimmung von Ableitungen oder Integralen sowie Potenzfunktionen, mit Exponenten, die nicht Elemente der natürlichen Zahlen sind genauso Simulationen in der Abiturprüfung Mathematik 2022 für den Grundkurs nicht gefordert.
Du wirst im Bereich z. B. Gleichungen und Gleichungssysteme folgende Verfahren und Gleichungen beherrschen müssen:
- Verfahren zur Lösung von linearen, quadratischen und biquadratischen Gleichungen sowie Gleichungen höheren Grades unter Verwendung der Polynomdivision und der Linearfaktorzerlegung
- natürliche Exponentialgleichungen unter Anwendung des natürlichen Logarithmus und der Logarithmengesetze für den natürlichen Logarithmus
- Gauß-Verfahren zum Lösen linearer Gleichungssysteme
- Lösbarkeit eines linearen Gleichungssystems (eine Lösung, keine Lösung, unendliche viele Lösungen)
- Wurzelgleichungen (nur im LK)
Alle Bereiche und deren Themen findest du in der Übersicht der Länder Berlin und Brandenburg zum schriftlichen Abitur 2022.
Titelbild: © sofatutor.com
- Motivation beim Lernen ist der Schlüssel zum Erfolg! Hole dir jetzt die Motivationstipps in diesem Video.
- Gehe auf Entdeckungsreise und schau dir an, wie sofatutor dir beim Lernen hilft.
- Sprich mit deinen Eltern und teste sofatutor 30 Tage lang kostenlos.
Weitere Verwandte Artikel
Kommentieren







Super Seite aber der Download klappt leider nicht